深入向量化计算技术

计算加速的技术

计算加速可以从多个方面入手。软件加速/硬件加速。从软件上来讲，尽可能的榨干硬件的性能；从硬件上讲，尽可能的提高主频。从方向上讲，可以横向扩展，使用更高的并发处理能力；或者在纵向上提高单点的性能。并发处理能力，从粒度上区分，从到小有机器级别的并发，堆机器做同样的事情；或者线程级别的并发，利用多线程多核并发计算；或者指令级别的并发，在一个指令上操作多个数据。

其他并发处理方式比较常见，那么指令级并发怎么理解呢？冯诺依曼式架构是CPU从存储系统中加载指令和数据，完成指令并把结果保存到存储系统。通常一个指令操作一个数据，生成一份结果。而SIMD(Single Instruction Multiple Data)指令是一类特殊的CPU指令类型，这种指令可以在一条指令中，同时操作多个数据。

SIMD指令的作用是向量化执行(Vectorized Execution)，中文通常翻译成向量化，但是这个词并不是很好，更好的翻译是数组化执行，表示一次指令操作数组中的多个数据，而不是一次处理一个数据；向量则代表有数值和方向，显然在这里的意义用数组更能准确的表达。在操作SIMD指令时，一次性把多条数据从内存加载到宽寄存器中，通过一条并行指令同时完成多条数据的计算。例如一个操作32字节(256位)的指令，可以同时操作8个int类型，获得8倍的加速。同时利用SIMD减少循环次数，大大减少了循环跳转指令，也能获得加速。SIMD指令可以有0个参数、1个数组参数、2个数组参数。如果有一个数组参数，指令计算完数组中的每个元素后，分别把结果写入对应位置；如果是有两个参数，则两个参数对应的位置分别完成指定操作，写入到对应位置。

编译器通过SIMD加速的原理是：通过把循环语句展开，减少循环次数，循环展开的作用是减少循环时的跳转语句，跳转会破坏流水线；而流水线可以预先加载指令，减少CPU停顿时间，因此减少跳转指令可以提升流水线的效率。

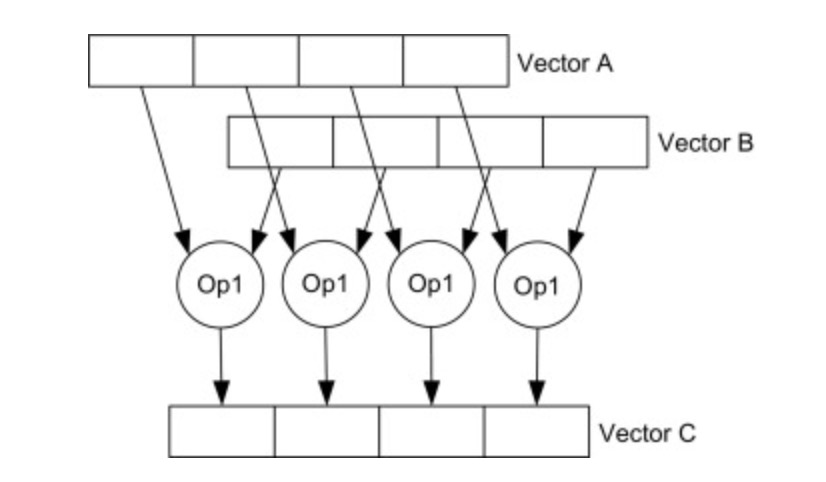
image-20221207094652357

图：SIMD指令同时操作A和B中4对数字，产生4个结果存放到C中

以如下代码为例，对4个float计算平方：

1
2
3
4
5
6
7
8
9

void squre( float* ptr )
{
		for( int i = 0; i < 4; i++ )
   	{
			const float f = ptr[ i ];
    	ptr[ i ] = f * f;
		}
}

上述代码转写成SIMD指令，则可以删除循环，用三条指令即可完成计算，分别是加载到寄存器，计算平方，结果写回内存:

1
2
3
4
5
6
void squre(float * ptr)
{
	  __m128 f = _mm_loadu_ps( ptr ); 
	  f = _mm_mul_ps( f, f ); 
     _mm_storeu_ps( ptr, f );
}

理论上，各种数据类型和指令宽度下的加速比如下表，在最好的情况，对char类型可实现64倍提速。

数据类型/指令宽度 128位指令 256位指令 256位指令
char(1byte) 16 32 64
int(4 byte) 4 8 16
long(8 byte) 2 4 8
float(4 byte) 4 8 16
double(8 byte) 2 4 8

SIMD扩展指令集

SIMD指令的运行方式时，把一组数据加载到宽寄存器(128位、256位、512位）中，然后生成结果放到另一个宽寄存器中。

SIMD指令需要硬件支持MMX系列，SSE(Streaming SIMD Extensions)系列、AVX(Advanced Vector Extensions)系列扩展指令集。SSE1、SSE2、SSE3、SSE4.1、SSE4.2操作的是16字节寄存器，AVX、AVX2引入了32字节寄存器，AVX512引入了64字节寄存器。目前大部分CPU都支持AVX2，只有最新的CPU才支持AVX512。

指令集需要CPU硬件支持，下标列出了支持各个指令集的CPU。

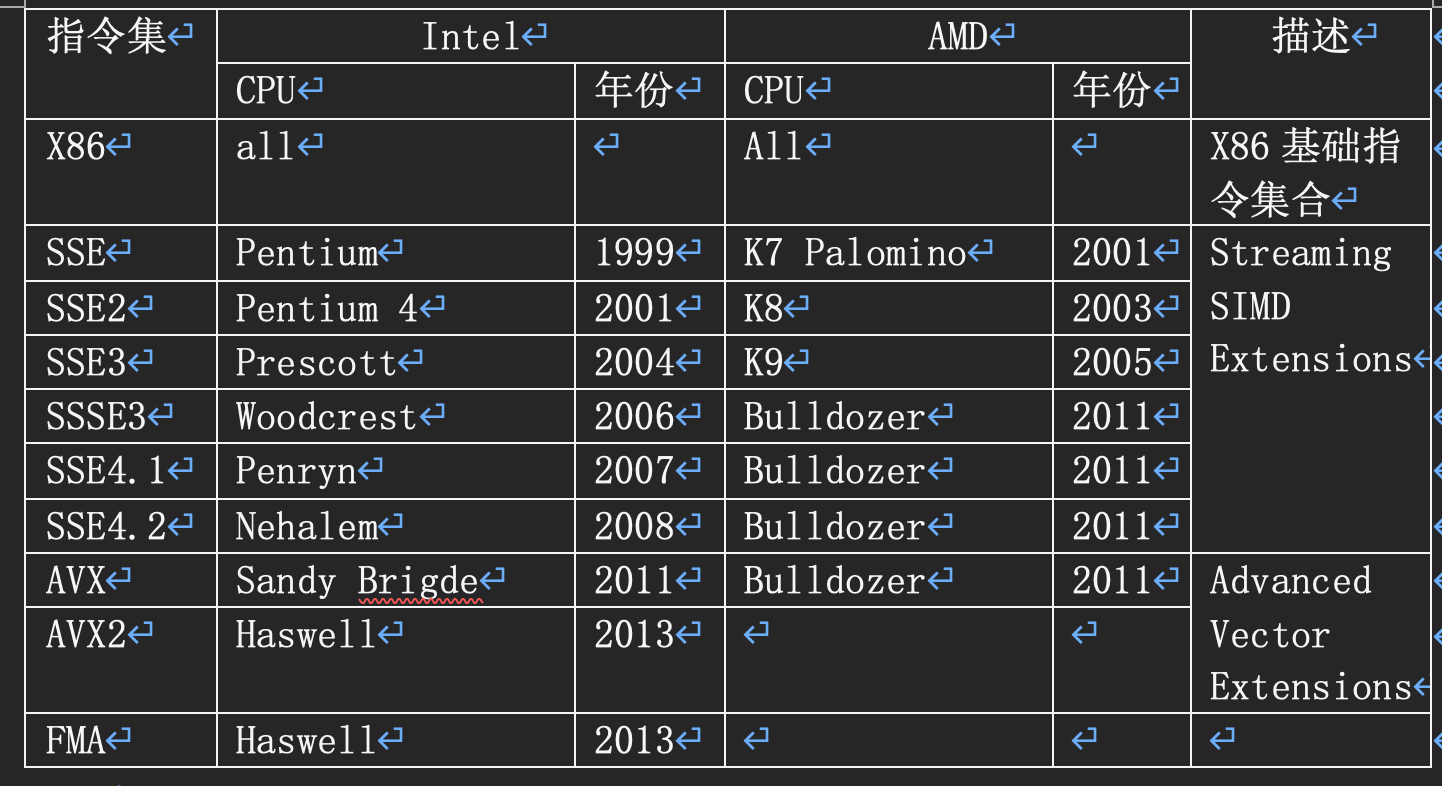
image-20220618163034294

ARM也引入了SIMD扩展指令。典型的SIMD操作包括算术运算(+-*/)以及abs、sqrt等，完整的指令集合请参考英特尔提供的使用文档https://software.intel.com/sites/landingpage/IntrinsicsGuide/#

那么如何生成SIMD指令呢？有几种方式：

  1. 编译器自动向量化：
    1. 静态编译。
    2. 即时编译（JIT）。
  2. 可以手写SIMD指令。

编译器静态自动向量化：

对于编译器自动向量化，需要有几个条件：

  1. 代码满足一定的范式。后续会详细展开介绍各种case。
  2. 对于常用的编译器入gcc和clang，在编译选项上加上-O3的选项，开启向量化。

编译器选择和选项

在编译时，编译选项中加上-O3或者 -mavx2 -march=native -ftree-vectorize，可以开启向量化。

只有高版本的编译器才能实现向量化，gcc 4.9.2及以下测试不支持向量化。gcc 9.2.1支持。gcc对向量化的支持更加友好，而clang对某些代码无法转化成向量化。而有些情况下，clang生成的向量化代码性能比gcc更好（采用更宽的寄存器指令导致的）。不一而足。因此，建议编写符合规范的代码，然后分别测试两种编译器的性能。

1
2
res[i] = tmpBitPtr[i] & opBitPtr[i];   //使用下标访问地址，clang和gcc都支持
*(res + i) = *(tmpBitPtr + i) & *(opBitPtr + i);  //使用地址运算访问内存，clang不支持，gcc支持

如何写出可向量化的代码：

为了更好的引导编译器给你的代码生成向量化代码，编程上有一些最佳实践。

1 循环的次数要是可计数的

循环的变量初始值和结束值要固定，例如

1
2
for (int i = 0;i < n ;++i ) //总的次数是可以计数的,这种写法可以向量化
for (int i = 0;i != n;++i) //总的次数不可计数，这种写法无法向量

2 简单直接的计算，不包含函数调用

计算只包含简单的加减乘除等数学运算、与或非等逻辑运算。不要包含switch，if，return等语句。

此处有一些例外是，部分三角函数(sin,cos等)或者算术函数(pow,log等)因为lib提供了内置的向量化实现，是可以自动向量化的。

3 在循环的最内层

只有最内层的循环可以向量化

4 访问连续的内存空间

也就是函数的计算参数和结果必须存放在连续空间中，通过一条simd指令从内存加载到寄存器。

1
2
for (int i=0; i<SIZE; i+=2) b[i] += a[i] * x[i];   //访问连续空间，可以向量化
for (int i=0; i<SIZE; i+=2) b[i] += a[i] * x[index[i]] //访问非连续空间，不能向量化

5 数据无依赖

这是最重要的一条，因为是并行计算，属于同一条并行指令的多个独立指令所操作的数字，之间不能有关联，否则就不能并行化处理，只能串行计算。

数据依赖有几种场景：

1
2
3
4
5
6
7
8
9
for (j=1; j<MAX; j++) A[j]=A[j-1]+1;// case 1 先写后读，不能向量化
for (j=1; j<MAX; j++) A[j-1]=A[j]+1;// case 2 先读后写，不能向量化
for (j=1; j<MAX; j++) A[j-4]=A[j]+1;// case 3 虽然是先读后写，但假如4组数据组成一个向量，那么同一组数据内无依赖的，因而可以向量化
                                     // case 4 先写后写，无法向量化（此处无案例）
for (j=1; j<MAX; j++) B[j]=A[j]+A[j-1]+1;//case 5 先读后读，因为没有写操作，不影响向量化
for (j=1; j<MAX; j++) sum = sum + A[j]*B[j] //case 6 这种可以向量化，虽然每次都会读同一个变量，再写一个变量，因为可以先用一个宽寄存器表示sum，分别累加每一路数据，循环结束后再累加宽寄存器中的值。
 for (i = 0; i < size; i++) {
 		c[i] = a[i] * b[i];
 }// case 7这种要确认c的内存空间和a/b的内存空间十分有交集。如果c是a或者b的别名，比如c=a+1，那么c[i] = a[i+1]，那a和c就有内存交集了。

上述几个例子中，case 3、5、6是可以向量化的，这些case属于比较特殊的case，正常而言建议还是写出明确无任何依赖问题的代码。如果确定有依赖，仍想使用向量化，可以手动编写SIMD代码。

6 使用数组而不是指针

尽管使用指针可以达到数组类似的效果，但是使用数组，可以减少出现意外依赖的可能。而使用指针的时候，有些场景下连编译器也无法确认是否可以向量化。使用数组则没有这种担忧，编译器可以很容易的向量化。

7 使用循环的计数器作为数组的下标

直接使用循环的计数器作为数组的下标访问，可以简化编译器的理解。如果额外的使用其他值作为下标，则很难确认能否向量化。例如

1
2
for(int i = 0;i < 10;i++)  a[i] = b[i] //这种较好
for(int i =0,index=0;i < 10;i++)  a[index++]=b[index] //这种无法向量化

8 使用更高效的内存布局

数据最好以16字节或者32字节对齐。数组的元素最好是基础类型，而不是结构体或类。如果是一个复杂结构，那么同一个数组中每个对象的相同元素并不是相邻存储的。

9 循环次数并不需要是指令宽度的整数倍。

在一些老的编译器中，循环的次数需要是指令宽度的整数倍，例如128位指令，操作4字节的int类型，可以同时操作4个int类型，那么就要求循环次数是4的整数倍。因此写代码时，需要写成两个循环，第一部分是4的整数倍循环；第二部分是末尾多出来的少量数据。

而最新的编译器以及能够自动化的处理这种情况，编写代码按照正常逻辑写就行，无需拆分成两部分。编译器生成的代码会自动生成两部分逻辑。

手写SIMD 代码

编译器能把直接了当的逻辑转换为SIMD指令，并且需要我们认真的考虑代码风格，避免阻碍向量化。但是有些比较复杂的逻辑，编译器是无法自动向量化的，而我们人类知道这里边的逻辑是每个操作数分别计算，互不干扰，可以使用向量化。这种情况，我们可以手写SIMD代码。举一个典型的例子，把一个字符串转成全小写。

SIMD代码例子和不同编译器性能对比

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
const static char not_case_lower_bound = 'A';
const static char not_case_upper_bound= 'Z';
static void lowerStrWithSIMD(const char * src, const char * src_end, char * dst)
{   
    const auto flip_case_mask = 'A' ^ 'a';

#ifdef __SSE2__
    const auto bytes_sse = sizeof(__m128i);
    const auto * src_end_sse = src_end - (src_end - src) % bytes_sse;
    
    const auto v_not_case_lower_bound = _mm_set1_epi8(not_case_lower_bound - 1);
    const auto v_not_case_upper_bound = _mm_set1_epi8(not_case_upper_bound + 1);
    const auto v_flip_case_mask = _mm_set1_epi8(flip_case_mask);
    
    for (; src < src_end_sse; src += bytes_sse, dst += bytes_sse)
    {   
        /// load 16 sequential 8-bit characters
        const auto chars = _mm_loadu_si128(reinterpret_cast<const __m128i *>(src));
        
        /// find which 8-bit sequences belong to range [case_lower_bound, case_upper_bound]
        const auto is_not_case
            = _mm_and_si128(_mm_cmpgt_epi8(chars, v_not_case_lower_bound), _mm_cmplt_epi8(chars, v_not_case_upper_bound));
        
        /// keep lip_case_mask _mm_and_si128(v_flip_case_mask, is_not_case);
        
        /// flip case by applying calculated mask
         const auto xor_mask = _mm_and_si128(v_flip_case_mask, is_not_case);
        const auto cased_chars = _mm_xor_si128(chars, xor_mask);
        
        /// store result back to destination
        _mm_storeu_si128(reinterpret_cast<__m128i *>(dst), cased_chars);
    }
#endif
    
    for (; src < src_end; ++src, ++dst)
        if (*src >= not_case_lower_bound && *src <= not_case_upper_bound)
            *dst = *src ^ flip_case_mask;
        else
            *dst = *src;
}
static void lowerStr(const char * src, const char * src_end, char * dst)
{   
    const auto flip_case_mask = 'A' ^ 'a';

    for (; src < src_end; ++src, ++dst)
        if (*src >= not_case_lower_bound && *src <= not_case_upper_bound)
            *dst = *src ^ flip_case_mask;
        else
            *dst = *src;
}

上述两个函数用于把字符串中的大写字母转换成小写字母，第一个函数采用了SIMD实现（采用128位指令），第二个函数采用了普通的做法。由于第一个是128位指令（16字节），理论上相比非向量化指令，加速比是16倍。但是由于第二个代码在结构上是很清晰的，也可以自动向量化，在这里我们测试下不同编译器的编译性能,g++版本9.3.0,clang++12.0.0

编译选项 SIMD/normal 延时比较 解读(延时比小于1则SIMD占有，大于1则后者的自动向量化占有))
g++ -O3 -mavx2 -march=native -ftree-vectorize 1.9 编译器自动向量化生成了256的指令，相比128位性能加倍
g++ -O3 0.99 两者近似，编译器自动向量化生成了128位指令
g++ -O2 0.09 -O2无法自动向量化
clang++ -O3 -mavx2 -march=native -ftree-vectorize 3.1 自动向量化生成了512位指令，相比128位性能3倍多
clang++ -O3 1.6 编译器自动向量化生成了256位指令
clang++ -O2 0.93 编译器自动生成了128位指令
clang++ -O1 0.09 -O1无法向量化

结论：在相同的优化级别下，clang生成更宽的指令，性能更好。

解读SIMD指令

最简单的SIMD指令，实现两个数字的加法:

1
const __m128i dst = _mm_add_epi32(left,right);

这条指令把4组int类型数字相加，填写到结果中。__m128i代表是128位宽寄存器，存放的是int类型（4字节32位），可以存放4个int类型。_mm_and_epi32是一个simd指令，_mm开头表示128寄存器，add表示相加,epi32表示32位整数。SIMD指令的命名规范：在SIMD指令中，需要表达三个含义，分别是寄存器宽度、操作类型、和参数宽度。

各种类型对应到各种宽度的寄存器上的写法：

16字节 32字节 64字节
32位float __m128 __m256 __m512
64位float __m128d __m256d __m512d
整型数 __m128i __m256i __m512i

寄存器宽度，例如128位寄存器以_mm开头,参考如下表格映射关系：

指令前缀 寄存器位数
_mm 128
_mm256 256
_mm512 512

操作类型，例如xor、and、intersect等操作。

参数宽度：参数中单条数据的位数，在指令的后缀中包含该信息，例如浮点数是32位，双精度浮点数是64位，那么在128位寄存器上，可以输入4个浮点数或者2个双精度浮点数。有些指令没有输入参数，则没有参数宽度信息。例如epi16代表16位int，详细的信息参考如下表格:

指令后缀 单条数据位数 数据类型
epi8 8 int
epi16 16 int
pi16 16 int
epi32 32 int
pi32 32 int
epi64 64 int
pu8 8 unsigned int
epu8 8 unsigned int
epu16 16 unsigned int
epu32 32 unsigned int
ps 32 float
pd 64 double

例如函数__m128 _mm_div_ps (__m128 a, __m128 b)，根据指令名称__mm开头，代表寄存器是128位，div表示除法，ps结尾代表操作的参数是32位浮点数。即同时加载两个数组，每个数组包含了4个32位单精度浮点数，完成两个数组对应位置数字的除法运算，返回4个除法结果.

通常，指令的结果宽度是和参数的宽度是保持一致的，但也有例外。

通常，两个向量执行SIMD指令，是两个向量的对应位置的数据分别执行操作。但也有些例外，比如同一个向量的相邻数据执行操作，称为水平操作，例如指令__m128i _mm_hadd_epi16 (__m128i a, __m128i b)，指令中的h代表horizontal，依次把a和b相邻的数据想加，如果a值为[1,2,3,4]，b值为[5,6,7,8]，那么结果为[1+2,3+4,5+6,7+8]。

通常，两个向量的所有数据都参与计算，但也有例外，通过掩码控制部分数据参与计算，掩码的第几位为1，则代表第几个数字参与计算。例如函数__m128i _mm_mask_add_epi16 (__m128i src, __mmask8 k, __m128i a, __m128i b)，用k作为掩码，第几位为1，则返回a和b对应位数的和；如果为0，则返回src对应位置的数。

SIMD 指令集合中包含的功能有：算术、比较、加密、位运算、逻辑运算、统计和概率、位移、内存加载和存储、shuffle。

1)SIMD内存操作

SIMD内存操作把数据加载到寄存器，并且返回对应SIMD类型。加载16位数据指令_mm_load_si128，加载64位数据指令：_mm256_load_ps，这两个指令要求数据是对齐的。如果是非对齐的数据，则采用_mm_loadu_si128和_mm256_loadu_ps。

2)SIMD初始化寄存器指令

初始化为0的指令。_mm_setzero_ps和_mm256_setzero_si256把寄存器初始化为0，初始化操作没有任何依赖。

初始化为特定值。_mm[256]_set_XXX把每一个点初始化不同的值，_mm[256]_set1_XXX 把每一个点初始化相同的值。[256]代表是否出现256，如果出现256。_mm_set_epi32(1,2,3,4)表示按照顺序初始化为整型数[1,2,3,4]。如果时倒序初始化，则使用_mm_setr_epi32(1,2,3,4)。

3)位运算指令

Float和int有很多位运算指令，包括AND、OR、XOR。如果要执行NOT指令，则最快的方式就是和全1做XOR，而获得全1的最快方式就是把两个0做相等比较。如下代码样例：

1
2
3
4
5
6
__m128i bitwiseNot(__m128i x)
{
	const __m128i zero = _mm_setzero_si128();
	const __128i one = _mm_cmpeq_epi32(zero, zero);
	return _mm_xor_si128(x, one);
}

4)浮点数指令

浮点数指令支持基础的运算+-*/，和扩展的运算sqrt。一些比较有用的函数有_mm_min_ss(a,b)， 对于32位浮点数，如果要完成img，对应的SIMD指令是_mm_rcp_ps，而img对应的SIMD指令是_mm_rsqrt_ps，采用SIMD指令可以在一条指令内完成，速度更快。

如果想加两个数组，例如[a,b,c,d]+[e,f,g,h]=[a+e,b+f,c+g,d+h]，对应的SIMD指令是_mm_hadd_ps，_mm_hadd_pd，_mm256_hadd_pd，_mm256_hadd_ps

5)非并行指令，却能做到加速效果

有些指令，在一条数据中只能操作一条数据，但是也能达到加速的效果。例如_mm_min_ss指令，表示取两个浮点数的最小值，该指令可以用一条指令完成计算，避免跳转，避免通过分支指令跳转。同理，取最大值的指令是_mm_max_sd。

手写SIMD指令的缺点

虽然手写SIMD指令看起来很酷，但是存在一个很大的问题是可移植性不强，如果你手写一个512位宽的指令，却在一个不支持avx指令集的机器上运行，那就会出问题。所以最好的方案还是编写符合编译器向量化规范的代码，把向量化这件事情交给编译器好了！最新的编译器会帮助我们解决这些事情。

结论

最新的编译器已经足够智能，能够自动化的实现向量化。而飞天长期使用4.1.2的编译器，最近一年才改到4.9.2，和最新的9.x编译器对比起性能，仍有比较大的差距。这种差距过于明显，是明显的代差，能够相差几倍。试想一下，代码不变的情况下，仅仅提升下编译器版本就能实现几倍的性能提升，这种结果过于震撼。因此提升编译器版本势在必行。

除了提升编译器版本，也需要提高开发者编写代码的能力，能够尽可能的编写出符合上文定义的几种规范，然后让编译器帮助我们生成高效的执行代码。

遗留问题：

c++ vector类型能否向量化。

foreach能否向量化

寄存器类型和数量

寄存器、内存体系结构。